As a decision maker you must know the Logistic Regression in detail. It enables you to solve the classification problems, Discrete Choice models. Besides that it enables you to compute the probability of an event occurs or not occurs. It plays an important role in Machine Learning and Predictive Analytics. Under machine learning we train the machine to learn about the data and to predict the value of dependent variable based on independent variables. Under Linear Regression (whether it be a simple and multiple linear regression), for finding out the regression coefficients we make some assumptions like 1) Residual errors follow normal distribution and 2) the variance of error term follows homoscedasticity and we used Ordinary Least Square Method. This OLS method is not applicable to Logistic Regression when we try to estimate the parameters (beta0, beta1, beta2,…betan). The Logistic Regression model is used when the target/response/dependent variable is in binary form. The dichotomous character assumes 0 or 1 (no or yes). That is only two values. We use MLE (Maximum Likelihood Error) method for estimating the parameters. Then we conduct different tests to know if the parameters are statistically significant or not to pass the model for deployment. The model thus found is to be carefully scrutinized very often, even after deployment, to valide the accuracy of the model.
Objectives:
Let us learn the following
- Classification problems and Discrete Choice models
- Logistic Regression
- Logistic function and logit function
- MLE (Maximum Likelihood Estimator). Used to estimate LR parameters
Classification Problem:
Examples:
- Customer Churn (for retaining existing customers companies may analyze the customer churn)
- Credit Rating. Banks may classify their borrowers based on the risk associated with them(low, medium, high)
- Employee attrition: Companies may wish to know which employee may leave the organization
- Fraud Detection: Bank may classify its customers transaction which are fraud prone
- Outcome of any binomial or multinomial experiment
Discrete Choice Models:
- Talks about the discrete choice available for making a decision
- Companies may want to identify which alternative brand is available in the market for retail customers and why
- Discrete Choice model estimates the probability of a customer to choose a particular brand among the available several brands in the market
Logistic Regression Solves:
- Classification problems
- Discrete Decision models
- Probability of an event occurs/not occurs
The classification problems can also be solved using
Classification problems can also be solved using
- Discriminant Analysis
- Decision Trees
- Classification Trees
- Neural Networks
However, the Logistic Regression is the best one.
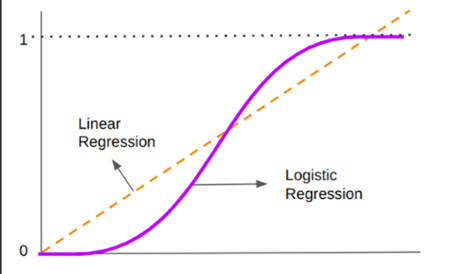
Logistic Regression
The name Logistic Regression comes from Logit function. The mathematical form of Logistic Regression is
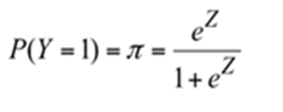
Logistic Regression tries to estimate the condition probability of an event happens. The probability of a customer who may churn (ie y = 1). This is what we are interested to know. We have only two values Y=1 or Y=0. In bank credit we are interested to know the probability of one borrower who may default ( Y=1). Y=0 is no default. We classify the borrower as default borrower and non-default borrower.
Under Binomial(binary) Logistic Regression model
- the dependent variable is dichotomous (takes only 1 or 0)
- the independent variables may be of any type
Logistic Function(Sigmoidal function)
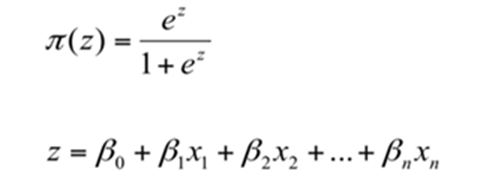
where
beat not, beta1, beta2… betan are LR parameters(coefficients)
x1, x2,x3,… xn are explanatory variables
- We estimate the LR parameters. 2. test 3. see if they are statistically significant or not . 4. assess if they influence the probability of an event occurs or not
Logistic Regression with one target and one explanatory Variable
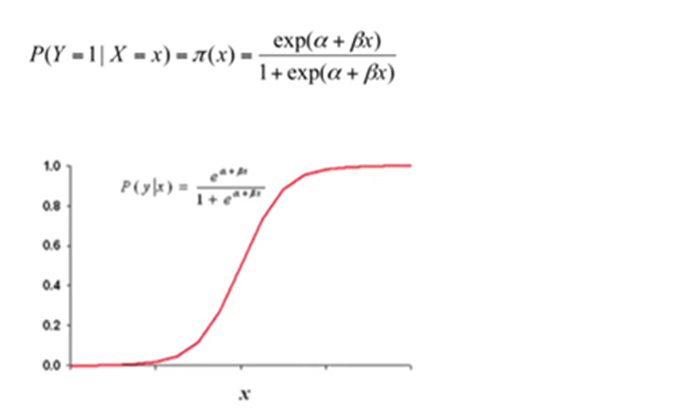
When B=0 it implies that P(y|x) is same for each value of x
When B>0 it implies that P(y|x) increases as the value of x increases
When B<0 it implies that P(y|x) decreases as the value of x increases
Logit Function
The Logit Function is the logarithmic transformation of a logistic function. Defined as the natural logarithm of Odds.
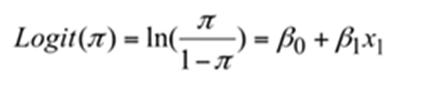
This form looks like a linear Regression.
On left-hand side we have a function which is continuous
On right-hand side we have linear function
Pi is the probability which is the probability of y=1

Odds = beta0 +beta1x
Robust
Logistic Regression is robust
Advantage over Linear Regression:
Assumptions made in Multiple Linear Regression are thwarted
-Residuals(error) need not follow normal distribution
-No requirement for equal variance for error term/residual(homoscedasticity assumption need not be taken)
Maximum Likelihood Estimator(MLE)
For estimating regression parameters in Linear Regression, we used Ordinary Least Square method. This is not applicable in Logistic Regression as many of our assumptions made in Linear regression are not valid here. It is a statistical model for estimating model parameters of a function. MLE chooses the values of model parameters that makes the data “more likely” than other parameter values.
Likelyhood Function: L(B) represents
the joint probability or likelihood of observing the data that have been collected.
MLE chooses that estimator of the set of unknown parameters which maximizes the likelihood function (L(B))
Assume x1,x2,x3,…xn some of the observations of a function f(x,θ) where ø is an unknown parameter
The likelihood function is L(θ) = f(x1,x2,x3…xn,θ ) which the joint probability density function(pdf) of the sample
The value of θ , θ* which maximizes L(θ) is called maximum likelihood estimator of θ
Exponential Distribution:
Let us assume x1,x2,x3…xn be the observations which follows exponential distribution with parameter θ.

log likelihood function
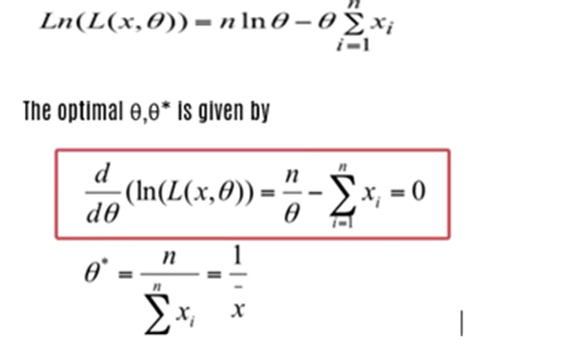
How likelihood function is used in Binary Logistic Function?

The above equations are to be solved to find beta0 and beta1 . It is very difficult. In linear regression we used standard normal equations and that was easy to solve.
LN PARAMETERS
Whether it be Linear Regression model or Logistic Regression mode we have to find out the parameters Beta 0, Beta1, Beta2…Beta n.
But in Logitic regression,we use different method to find out the same
Before that we must know Odds and Odds Ratio
For Logistic Regression model we use Logit functionO

ODDS
Odds is nothing but a ratio of two probability values

ODDS RATIO
Odds Ratio is nothing but a ratio of two odds
Beta coefficients: Beta not and Beta one
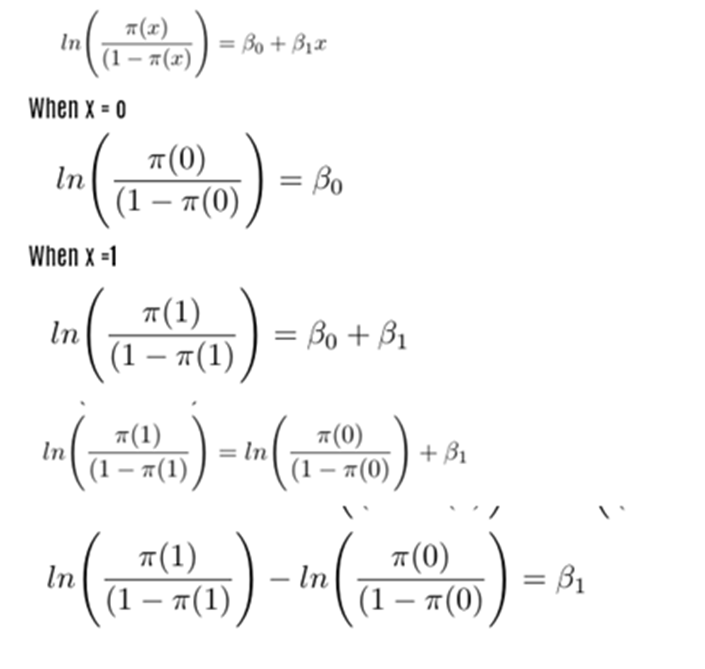
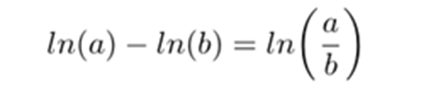
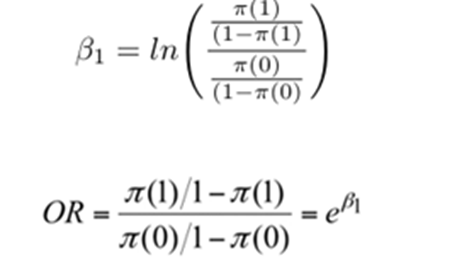
If OR (Odds Ratio) = 2 the event is likely to happen twice when x =1
OR approximates the relative risk
The relative risk either increases or decrease as the value of x increases or decreases
Beta 1 is the change in log odd ratio for a unit change in the explanatory variable
Beta 1 is the change in odd ratio by the factor exp(B1)